Skip to main content

Analyzing the MMR40 PTO – Manual Calculations

 

Analyzing the MMR40 PTO – Manual Calculations

Filed in Kits on Jan.25, 2009

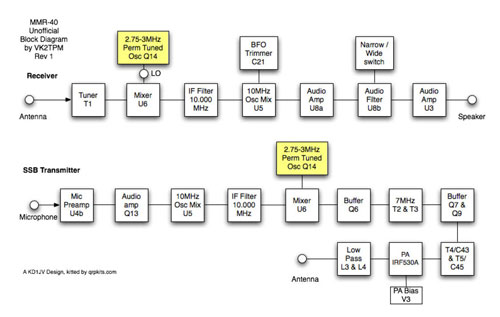
The MMR40 Permeability Tuned Oscillator is the variable frequency control for the rig.
It is used as one of the frequency sources for the first mixer(closest to the antenna), with the other source being the receive signal in receive, or the 10Mhz IF signal in transmit.


MMR40 PTO Block Diagram

The PTO consists of the following components:

  • Q14 Oscillator Transistor
  • D1 rectifier for AGC negative bias to Q14 gate
  • R2 Load Bias Resistor
  • C1 Coupling/Blocking Capacitor
  • C4 and C8 Frequency Determining Capacitors
  • S2 Band Segment Switch
  • L1 Frequency Determining Permeability Tuned Inductor
  • L2 Frequency Determining Fixed Toroid Inductor
  • C9 Bypass Capacitor
  • R1 Current Limiting Resistor

MMR40 PTO Schematic

Q14 is a J310 fet configured as a Hartley Oscillator. The oscillator is tuned by a brass screw through the middle of Inductor L1. In order to limit the number of turns on L1, the torrid L2 is wound with additional turns. The PTO has about 130khz of tuning range, given the capacitance of C8 to work with. By attaching capacitor C4 in parallel with C8, we are provided with a second range of approximately 130 kHz in the lower range of oscillation.

The inductive reactance of L1/L2 would ideally be about 100 ohms at the resonant frequency, according to EMRFD (Experimental Methods for Radio Frequency Design by Wes Hayward).
R2 acts as a load on the tank circuit, and a discharge path for blocking capacitor C1.
The Total tank capacitance is (C4 and C8 sometimes paralleled)

Calculating L2 Inductance:
39 turns on a T37-2 core
Diz's Website Toroid Windings Page gives us the formula and some tables to determine inductance from Core Type and number of turns.
The T37-2 core has an Al value of 40. The formula for inductance here is uh = (AL * Turns2) / 10000
uh = (40 * 28^2)/10000
uh = (40 * 784)/10000
uh = (31360)/10000
uh = 3.136

Calculating L1 Inductance:
From the Arrl Handbook, L1 inductance (without the brass screw) is determined by the formula uh =(d^2 * n^2)/((18 * d)+(40 * l)), where:
d = diameter of coil in inches
l = coil length in inches
n = number of turns

L1 is wound on a #6 nylon spacer, which is hexagonal in shape. Using my micrometer, the diameter from flat side to flat side is 0.260 inches. From corner to corner, it is 0.285 inches. I’ll assume an average diameter of 0.2725 inches. The length of the coil is about 0.385 inches.

So, plugging in our values:
uh = ((0.2725^2)*(39^2))/((18 * 0.2725)+(40 * 0.385))
uh = (0.07425625 * 1521)/(4.905 + 15.4)
uh = 112.94/20.305
uh = 5.562

Inductances add in series, like Resistances, so we have a total of 8.698 uh

Calculating our Resonant Frequency:
So let's see if we are in the right ballpark
The Tank Resonant Frequency is given by 1/((2*PI)(sqrt(L*C)))
Substituting our values gives us:
F = 1/((6.28)*(sqrt(0.000008698 * .000000000330))
F = 1/((6.28 *(sqrt(0.0000000000000000287034))
F = 1/(6.28 * 0.000000053576)
F = 1/0.0000003366
F = 2.970663 Mhz
So this is very close to the design frequency range of 2.75 - 3.00 MHz.

The inductive reactance of the 8.698uh total inductance at 2.875mhz would be:
(2)(PI)(F)(L) = 2 * 6.28 * 2875000 * 0.000008698
= 157 ohms, very close to the 100 ohms recommended by EMRFD.

 

Migrated Comments:

One Response to “Analyzing the MMR40 PTO – Manual Calculations”

  1. KD8JBX Says:
    May 5th, 2011 at 2:11 am

    oops, found them here sir 🙂 Thanks a ton for this information!

 

Comments

Post a Comment

Popular posts from this blog

Building the W8NX Short Trap Dipole

Image
  Building the W8NX Short Trap Dipole Filed in Antennas on May.31, 2021 For the past five years, I have been operating the lower bands (30, 40 and 80 meters) with a trap dipole that was modeled after a web article written by John DeGood NU3E. [1] While the antenna performed well, a monsoon storm last summer beat it up enough that the antenna wire broke at the center balun. So I climbed the tower and lowered the remains of the antenna to the ground for repairs. On closer examination, I discovered that the relentless Arizona sun had taken its toll on the traps. The insulation on the exposed ends of the coax had rotted away. They were still working, but would need to be rebuilt and weatherized to insure good operation many years into the future. Since I was going to have to rebuild the antenna, I started thinking about whether this antenna met my current needs and wishes. I had been wanting to get on 160 meters at this QTH for some time, but my small back yard would
Read more

Yaesu G-450XL Rotator Repair

Image
  Yaesu G-450XL Rotator Repair Filed in Antennas on Dec.30, 2007 In December of 2007, the rope support for the center element of my Cushcraft A3 broke, requiring me to climb the tower and bring the beam down for maintenance.  At the same time, at had been noticing that the rotator control was not indicating correctly, it was very erratic.  So I brought the rotator down for maintenance, as well. The first step was to mark the side of the case, where the top and bottom of the clam shells connected together.  This would allow me to assemble it in the correct alignment when the time came.   Marked Case of Rotator Next, I took the top cover off.  All of the bearings between the clam shells in the depression on the outside were safely stored.   Top Removed A little inspection revealed what the problem was.  The center gear had broken away from the shaft it was pressed onto.  I tried re-pressing it back onto the shaft, but it was too worn out.  I found the phone number for p
Read more

JuncTek Battery Monitor MQTT Controller

Image
 I recently installed some 48 volt Lithium Iron Phosphate battery packs at the Ranch to replace the 9 year old Lead-Acid batteries that had started to fail.   eg4-lifepower4-battery-48v-100ah   These are rack-mount battery packs that are intended for powering computer servers.  They are reported to work very well in an off-grid power system.  The Problem I had a problem to solve before the upgrade, in that the old 48 volt inverter I had been using in our solar power system required a programming interface to change its operating parameters to match the new battery specifications.  Unfortunately, the manufacturer wants over $400 for the required interface to make these changes.  I am unwilling to pay this extortion money for a simple device that should cost less than $100. The communications protocol and interface is proprietary, so it would take a considerable effort to hack the interface. There are two sets of parameters in dealing with the inverter/battery connections: 1. The chargin
Read more